Blog
December 17, 2020

PyTorchでt-SNEを実装

概要

高次元データの可視化によく用いられるt-SNEの動作を理解するために、論文を読んで実装してみることにしました。パラメータ更新時の勾配計算で楽をしたいのでPyTorchで実装します。

基本的には元論文を参考に実装を行いました。

今回使ったコードはGithubにあげています。

t-SNE自体の解説記事ではありません。そのためt-SNEを既にある程度理解しているものと想定しています。

SNE

t-SNEには前身であるSNEなる手法が存在し、t-SNEはSNEの弱点を補った手法です。そこでまずはSNEを実装します。

詳細は論文を参考して頂きたいのですが、大まかな流れは以下の通り。

  1. $ y $ をランダムに初期化

  2. 高次元空間の各データポイントに対応する正規分布の分散を指定されたperplexityから求める。

  3. 高次元空間における各データポイント間の類似度を求める。

  4. 収束するまで以下を繰り返し

    • 低次元空間における各データポイント間の類似度を求める。
    • 高次元空間と低次元空間における類似度の分布が近づく方向へ $ y $ を更新

perplexityですが、高次元における各データポイントの類似度 $ p_{j|i} $ を自分以外の全ての $ j $ について求めたもののシャノンエントロピーとして定義されています。

つまりは、SNEは高次元の類似度を低次元でも保つように低次元表現を学習しますが、その高次元の類似度を算出する際に各データポイントの近傍をどれくらいまで考慮するのか、ということを調節していると考えられます。

極端に考えれば、perplexityをめちゃくちゃ小さくすると各データポイントの類似度のエントロピーが小さいことを意味するので、対応する正規分布の分散は小さいものに設定している、つまり本当に近傍にあるデータポイントのみを考慮して類似度を算出していると考えられます。

詳しくは論文を参照ください。

注意点

from itertools import product

import numpy as np
import pandas as pd
from sklearn.datasets import load_digits
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from tqdm import tqdm
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt

class SNE:
    def __init__(self, n_components, perplexity, lr=0.01, n_epochs=100):
        self.n_components = n_components
        self.perplexity = perplexity
        self.lr = lr
        self.n_epochs = n_epochs

    def _compute_perplexity_from_sigma(self, data_matrix, center_idx, sigma):
        similarities = self._similarity(data_matrix[center_idx, :], data_matrix, sigma, "h")
        p = similarities / similarities.sum()
        shannon = - (p[p != 0] * torch.log2(p[p != 0])).sum()  # log(0)回避
        perp = 2 ** shannon.item()
        return perp

    def _search_sigmas(self, data_matrix):
        sigmas = torch.zeros(self.N)
        sigma_range = np.arange(0.1, 0.6, 0.1)
        for i in tqdm(range(self.N), desc="search sigma"):
            perps = np.zeros(len(sigma_range))
            for j, sigma in enumerate(sigma_range):
                perp = self._compute_perplexity_from_sigma(data_matrix, i, sigma)
                perps[j] = perp
            best_idx = (np.abs(perps - self.perplexity)).argmin()
            best_sigma = sigma_range[best_idx]
            sigmas[i] = best_sigma
        return sigmas

    def _similarity(self, x1, x2, sigma, mode):
        # SNEでは高次元でも低次元でも正規分布を用いる
        return torch.exp(- ((x1 - x2) ** 2).sum(dim=1) / 2 * (sigma ** 2))

    def _compute_similarity(self, data_matrix, sigmas, mode):
        similarities = torch.zeros((self.N, self.N))
        for i in range(self.N):
            s_i = self._similarity(data_matrix[i, :], data_matrix, sigmas[i], mode)
            similarities[i] = s_i
        return similarities

    def _compute_cond_prob(self, similarities, mode):
        # SNEではmodeにより類似性の計算変わらない
        cond_prob_matrix = torch.zeros((self.N, self.N))
        for i in range(self.N):
            p_i = similarities[i] / similarities[i].sum()
            cond_prob_matrix[i] = p_i
        return cond_prob_matrix

    def fit_transform(self, X):
        self.N = X.shape[0]
        X = torch.tensor(X)

        # 1. yをランダムに初期化
        y = torch.randn(size=(self.N, self.n_components), requires_grad=True)
        optimizer = optim.Adam([y], lr=self.lr)

        # 2. 高次元空間の各データポイントに対応する正規分布の分散を指定されたperplexityから求める
        sigmas = self._search_sigmas(X)

        # 3. 高次元空間における各データポイント間の類似性を求める。
        X_similarities = self._compute_similarity(X, sigmas, "h")
        p = self._compute_cond_prob(X_similarities, "h")

        # 4. 収束するまで以下を繰り返し
        loss_history = []
        for i in tqdm(range(self.n_epochs), desc="fitting"):
            optimizer.zero_grad()
            y_similarities = self._compute_similarity(y, torch.ones(self.N) / (2 ** (1/2)), "l")
            q = self._compute_cond_prob(y_similarities, "l")

            kl_loss = (p[p != 0] * (p[p != 0] / q[p != 0]).log()).mean()  # log(0)回避
            kl_loss.backward()
            loss_history.append(kl_loss.item())
            optimizer.step()

        plt.plot(loss_history)
        plt.xlabel("epoch")
        plt.ylabel("loss")
        return y.detach().numpy()

結果

digitsデータを使ってPCAとSNEによる二次元への次元圧縮の様子を見てみます。

digits = load_digits()
X, y = digits.data[:200, :], digits.target[:200]
print(X.shape, y.shape)
>> (200, 64) (200,)

計算が重いのでサンプリングしてます。

まずはPCA

sc = StandardScaler()
X_sc = sc.fit_transform(X)

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_sc)

def plot_result(x_transformed, y, title):
    fig, ax = plt.subplots(figsize=(6, 6))
    colors = ['r', 'g', 'b', 'c', 'm', 'y', 'k', 'pink', 'orange', 'purple']
    for c, label in zip(colors, digits.target_names):
        ax.scatter(x_transformed[y == int(label), 0], x_transformed[y == int(label), 1], color=c, label=label)
        ax.legend()
        ax.set_title(title, fontsize=16)
    plt.show()

plot_result(X_pca, y, "PCA")

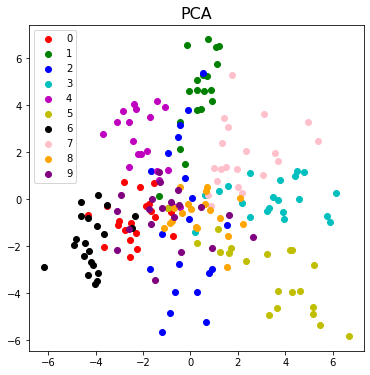
かなり重なりが多く、データの構造をうまく二次元へ落とし込めていないように見受けられます。

次にSNEですが

sne = SNE(n_components=2, perplexity=50, n_epochs=200, lr=0.1)
X_sne = sne.fit_transform(X_sc)

plot_result(X_sne, y, "SNE")

100イテレーションくらいで大体収束してるのがわかります。

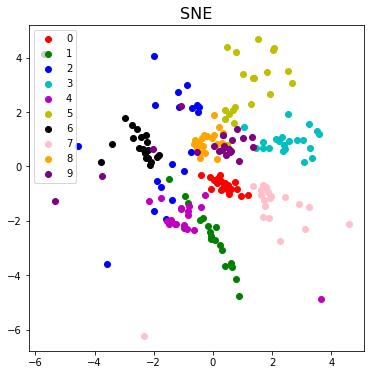
全体としてはPCAよりも各数字がギュッとまとまっており、重なりも少なく、データの構造をよく捉えているように見えます。

t-SNE

いよいよt-SNEですが、SNEまで実装してしまえば、大したことはありません。

主な変更点は以下の二つです。（詳細は論文を参照願います）

実際、上記の2点以外はSNEと基本的に同じなのでSNEクラスを継承します。

t-SNEでは先ほども述べたように、低次元と高次元で類似度の算出方法が異なるのでその部分の変更を加えます。

class TSNE(SNE):
    def _similarity(self, x1, x2, sigma, mode):
        if mode == "h":
            return torch.exp(- ((x1 - x2) ** 2).sum(dim=1) / 2 * (sigma ** 2))
        if mode == "l":
            return (1 + ((x1 - x2) ** 2).sum(dim=1)) ** (-1)

    def _compute_cond_prob(self, similarities, mode):
        cond_prob_matrix = torch.zeros((self.N, self.N))
        for i in range(self.N):
            p_i = similarities[i] / similarities[i].sum()
            cond_prob_matrix[i] = p_i

        if mode == "h":
            cond_prob_matrix = (cond_prob_matrix + torch.t(cond_prob_matrix)) / 2
        return cond_prob_matrix

結果

tsne = TSNE(n_components=2, perplexity=50, n_epochs=500, lr=0.1)
X_tsne = tsne.fit_transform(X_sc)

plot_result(X_tsne, y, "t-SNE")

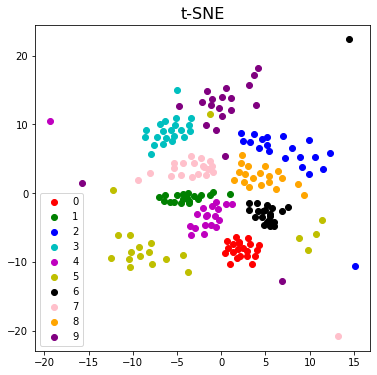
どうでしょうか？

主観ですが、各グループごとのまとまり・各グループ間の分離ともにかなりいい感じになり、 より見た目がすっきりした感があります。（SNEはごちゃごちゃ全体が固まっている感じ、論文でcrowding problemと呼ばれているもの？）

perplexityの値は割と敏感らしいのでもう少し調節しても良いと思いますが、とりあえずそれっぽい結果が出ているのでとりあえずここまでにしようと思います。

ちなみに、青色で表されている2がうまくまとまってないのですが、これは今回のデータの中にかなり性質の違う2たちが混在していたことによるようです。（文字の傾きにかなりばらつきがある）

TODO

何か間違い等ありましたら遠慮なくご指摘ください。

Follow me

誤りやコメントなどがあればご連絡ください。